Pythagoras and the Pythagorean brotherhood
The cycle “Ancient Philosophy: Formation of the Canon”:
- Introduction (Thales, Anaximander).
- First part (Pythagoras) — you are here.
- Second part (Xenophanes).
- Third part (Heraclitus).
- Fourth part (Parmenides).
- Fifth part (Summary).
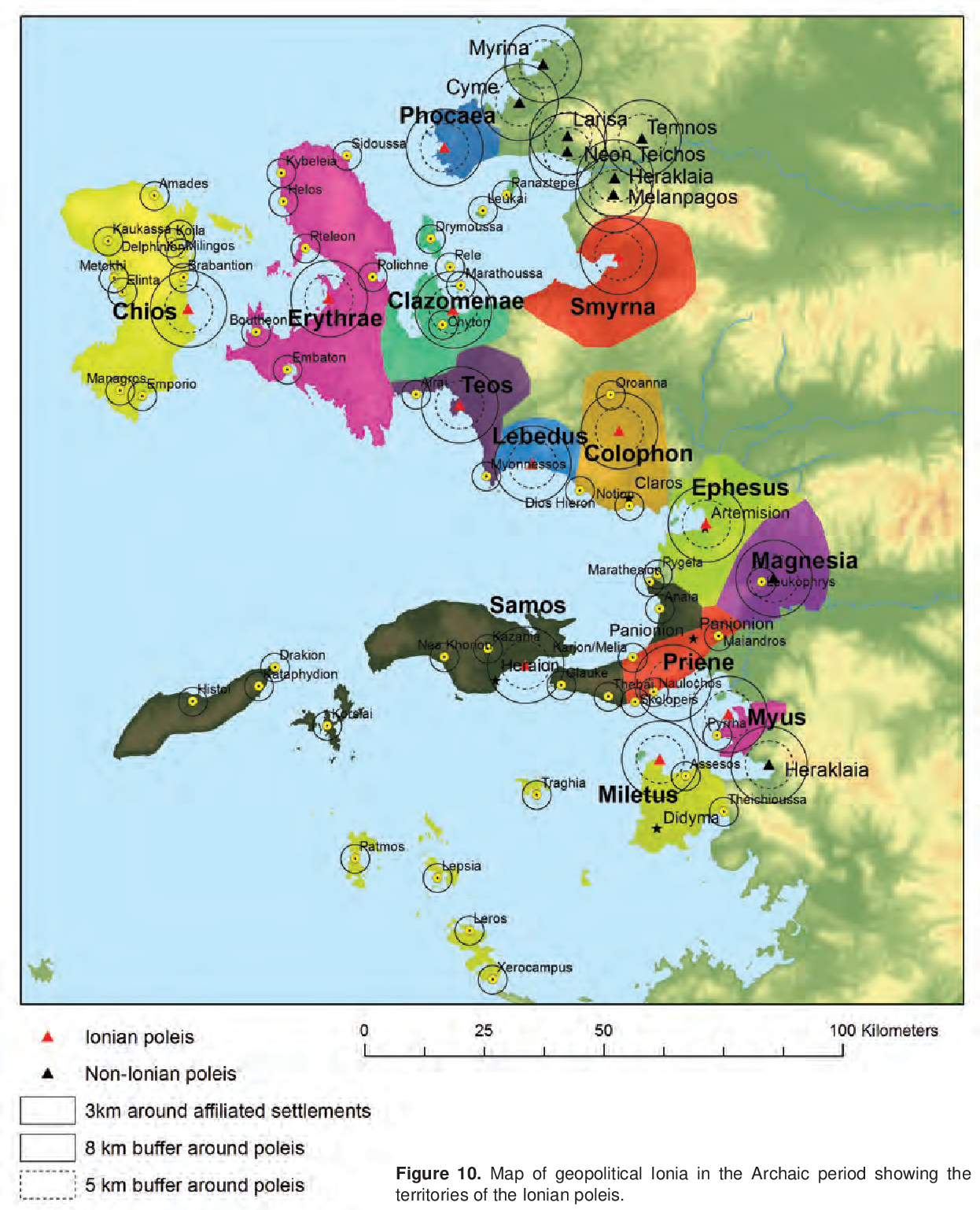
Now we know that the entire poetic culture, the Greek literary language itself, and with it the richest polities, including Miletus, the main colonial center of the Greeks, are all located on the Ionian coast. It is therefore no coincidence that this is where “philosophy begins”. However, already during the lifetime of Anaximenes, this abundance comes to an end. In 546 BC the Lydian kingdom was destroyed by the Persian king Cyrus, and his famous and sung by Greek poets capital Sardis fell. Croesus himself was most likely burned at the stake, and according to legend, already captured, he said the following words to Cyrus: “If you are victorious and your soldiers are plundering Sardis, they are plundering your property”. With this, Croesus supposedly stopped the plundering of his capital. There are also versions that Croesus was pardoned, and that he went to the court of the king as an advisor. Both versions, of course, are not very plausible, but legends about the fabulous wealth of his grandson (Pythias) — still hint that the family of the king subsequently received recognition from the new power. The Greeks of the Ionian coast also submitted to the new power.
During this period, the cultural ties of the Near East were seriously expanded. For example, before his defeat, Croesus had time to conclude treaties of alliance with Babylonia and Egypt, as well as a treaty of assistance with Sparta. Organizing an international coalition was no longer a difficult problem (although it had not been a problem long before, even in the Bronze Age); soon the ties between regions were further intensified, now by the incorporation of all the civilized regions of antiquity into the new single state. As for the Greeks, after the defeat of Croesus, the Ionian polities also became part of the Achaemenid Persian Empire. Even shortly before the invasion, the ruler of Miletus tried to reorganize the Ionian union, as it is believed, under the influence of his political advisor Thales, as we have already discussed before. But there was little effect, for the alliance turned out to be purely nominal, and the same Thales advised at the last moment not to oppose Persia in order to keep the city intact. “Loyalism” of Thales can also be questioned, since the last traces of Thales and Anaximander (presumably the years of their death) are almost synchronous in time with the Persian invasion. It is quite possible not only their political influence on the life of the city, but also their attempts to organize resistance, which was followed by retaliatory repression in their direction. There is, of course, no direct evidence of this. But this is roughly how the “Miletian School” left the scene.
The last representative of the Miletus school, and the only philosopher who lived in the region at this time, was the already known to us “philosopher of the air” Anaximenes. For a time, however, two other significant thinkers caught this era, Pythagoras of Samos and Xenophanes of Colophon. It was they, and not Thales or Anaximander, who were destined to lay the foundation for the development of the entire further philosophical tradition. In fact, it is true that Pythagoras and Xenophanes simply continued the ideas of the Miletians, but if we compare them, then even from the scanty passages that have come down to us, we can feel a significant difference. And if we think within the framework of the old Marxist classification — then both Pythagoras and Xenophanes will appear against the background of Anaximander as “idealists” against the background of “materialist” (of course, it is very conditional). Consequently, the foundation on which the further philosophy of antiquity was built was the foundation of the victory of early idealism. On the contrary, materialist philosophy had now to rise from literally nothing, overcoming the resistance not only of mythology and religion, but also of the “philosophical canon” itself. We will try to find out what this “canon” is in this article.
Journey to the West
After the Persian conquest of Ionia, the center of ancient philosophical thought moves to “Greater Greece” (Southern Italy). This was a backward agricultural region made up of colonies and predominantly inhabited by local natives with a more rural and archaic culture. It was here that refugees from the east evacuated. Of course, even here among the new polities there are regional leaders (Croton, Tarentum, Syracuse) capable of competing with the main polities of Greece; but all these exceptions are five-minute colonies that continue to exchange grain for handicrafts from the “center”.
Just in one such center in Italy, Pythagoras (ca. 570-490 B.C.), the son of a master jeweler, founded his philosophical school. But Pythagoras would not leave the island of Samos until around 530 BC, when he must have been about 40 years old. Obviously, by this time some philosophical positions must have already formed in his mind. And since his home island was not far from Miletus, and the years of his life allow it, we can safely say that Pythagoras became personally acquainted with geometry through Thales. Besides, there is evidence from ancient authors about their personal meetings, and even about the influence of Anaximenes on the question of animating bodies. It is often admitted that the philosophy of Pythagoras was borrowed from the East, first of all from Egypt, where he was allegedly directed by Thales himself. But at that, purely biographically, the voyage to Egypt (and further to Babylon and even India) looks a bit strange, as it does not quite coincide with the dating of his life. But even a trip to India was not something impossible for that time; the only problem is that Pythagoras had a lot of time to do in Europe, and from somewhere he found more time than a man engaged in such distant expeditions could get.
But, as we see, for acquaintance with Egypt it was not necessary for him to go there physically. Thales knew eastern sciences, and transferred them to Greece. Some elements of eastern cosmogony (the theory of creation of the world) are present in Anaximander. Therefore, in any case, whether he traveled somewhere or not, his knowledge may well have had Eastern roots.
The main premise on which we base our consideration of the Pythagoreans is this: by the time Pythagoras decides to leave his homeland, the basic foundation of his knowledge is entirely “Miletian” in character. In a sense, Pythagoras continues the tradition of the Miletian school, while founding his own. He synthesizes the teachings of Thales, Anaximander and Anaximenes (as we will see further on with specific examples) with the philosophy of Pherecydes and the religious ideas of the Greeks and Egyptians.
Pythagoras also, like his predecessor philosophers, was interested in politics, even tried to take an active part in it. And if to generalize the political vector of Pythagoreanism — it is an extremely conservative philosophy. Pythagoras himself fled to Italy, because at that time a tyrant ruled on Samos. This can be interpreted as an example of libertinism, as a criticism of tyranny; but in the context of his era, tyrannies were a form of struggle of the townspeople against the large landed aristocracy. The protest against tyranny may indicate that Pythagoras was a supporter of the power of the aristocracy (for the same reason the philosopher Xenophanes emigrates, by the way). He realized that he had no political future in his homeland, and either he was expelled or he left there himself. Note that despite the ethical conservatism of the Miletian philosophers, politically and economically they were not opposed to tyrants; rather, even on the contrary, they catered to their rule. But as in philosophy, Pythagoras proved to be a true innovator even in political conservatism. When he arrives in Italy, he establishes there a special organization, the likes of which had never been seen before; a kind of secret political alliance. We will begin with this episode of his life, especially since he most likely based his philosophical school on the foundation of a political union.
Pythagorean brotherhood
Here it is important to emphasize once again that Miletus at that time was the largest city of the entire Greek world, the richest trade and maritime center. Of all the Greek colonies in the Black Sea — 95% belonged to this city. Against this background, Italy was an agricultural and colonial region, a backward province, at least at first. And what are the Orphic and Dionysian cults (well, let’s not forget the mysteries) but agricultural cults originating from the common people? Who is more likely to preach unity with nature — city dwellers or villagers? This is a rhetorical question, the answer to which is obvious. It should always be kept in mind that the question of the difference between the city and the countryside is a very important one, also for philosophy; it is so obvious that not only the ancient Greeks, but even the Sumerians and Egyptians did not avoid this question (see the Sumerian myth of how Enkidu became a man). As lifestyle influences one’s ideas, so too the surroundings of the sages from Miletus (i.e. the leading metropolis) and the life of Pythagoras (i.e. the rural outskirts) — left their imprints on their philosophy. Much of the strange legends about the “religion” of the Pythagoreans may well be the results of a syncretism of Eastern sciences and the common folk beliefs of the Greeks. It remains only to understand why quite educated Pythagoras became a spreader of superstition.
Early sources, including Aristotle, tell us almost nothing about Pythagoras himself, but speak a lot about the “Pythagorean way of life” and numerous Pythagoreans. Unlike the Ionian philosophers, Pythagoras managed to create a full-fledged mass school, where both men and women were admitted, perhaps even from different classes (but most likely only aristocrats). In this respect his activity can be considered as the first example of Enlightenment. Of course, Pythagoras himself acquired his education while he was living near Miletus; but one must keep in mind that to succeed among the public, one must say what the public is interested in. And if the local population of Italy is interested in religious mysticism, they will have mysticism. If they want fantastic stories, they will have stories. Pythagoras positioned himself to be a constant source of delight and shock for the public. His most famous adventure (more of them have survived, as you can read about in primary sources) was that he built himself a room underground, and ordered his mother to spread rumors that he was dead. In doing so, she was to write down on a slate everything that happened upstairs, noting the time of events, and then bring it down to him. Later he returned upstairs, looking as skinny as a skeleton, and came to the people’s assembly, where he announced that he had come straight from Hades. At the assembly he read out everything that had happened during his absence. All those present were so excited that they rushed to weep and even believed that Pythagoras was a divine being. And he himself later emphasized in various ways that his nature was different from ordinary human nature, and was somewhere between men and gods.
This calculation for the involvement of the masses could be the reason for the sectarian division of the school into several levels. Such measures are useful to separate the “mass” from the chosen sages, but at the same time not to close access to the uninitiated (otherwise it would be impossible to maintain the mass of the organization). Successful propagation requires inducing a sense of ownership in the followers, and Pythagoras did this successfully. Ancient sources report that the property of the Pythagoreans became common, and their daily routine was clearly regulated and included joint meals, walks, and study (cf. ancient Sparta). The adherents of the school swore that they would strive for the knowledge of truth, which implied, among other things, religious rites, ascetic lifestyle, and the study of philosophy. Knowledge in the community was passed on only to recognized members. Disclosure of information to the uninitiated entailed banishment. Pythagoreans used secret signs, thanks to which they could find fellow believers in different cities. Because of all this, their organization is compared to the prototype of Christian monasteries and Masonic lodges.
The School of Pythagoras, founded around 525 B.C. (and destroyed 75 years later, around 450), is divided into ethical-political and scientific-philosophical communities. It is most likely that the latter is based on the foundation of the former, and that Pythagoras originally built something resembling a political party, united by ethics like a religious order. The fact that Pythagoras himself was a conservative in the field of politics, affects the positions of the whole Pythagorean union, and even the internal organization of the party. Explicit borrowings of Spartan orders, as well as a disdain for the lower classes and a love of hierarchical subordination, were dictated by this conservatism. Believing that the masses of people were too stupid — the Pythagoreans proposed, instead of the old democracy and monarchy — the rule of a group of wise men (i.e. themselves). Although in fact it was little different from aristocratic rule, Pythagoras was the first theorist of an enlightened meritocracy. And what is more important, unlike Plato, he succeeded!
The first important event for the Pythagoreans was the war between Croton and Sybaris (later known for its legends of corruption and wastefulness). After the tyrant Telis seized power in Sybaris, his opponents fled to Croton. The Crotonian council under the influence of Pythagoras refused the embassy from Sybaris to extradite the fugitives and started a war to restore order. The Crotonian army, under the command of the Pythagorean Milon, about 510 B.C. defeated the Sybarites, and their city was sacked and destroyed with the utmost cruelty. After the victory, Croton became the most powerful among the cities of southern Italy, and the other polis became its forced allies. The role of the Pythagorean Union also increased. However, the power of the secret society of Pythagoreans caused discontent. Therefore, a certain Kilon used the discontent with the authoritarian policy of the Pythagoreans and, perhaps, the unfair division of the land taken away from the Sybarites (or perhaps it was simpler, as later with the Jews — people were not satisfied with the closedness of the sect, which led to rumors about eating babies, etc. things). Together with his supporters, Kilon attacked the Pythagoreans during their convention in Crotona, burned down the meeting place and killed many of them, and many fled for their lives. According to another, less widespread version, Kilon attacked the school after it had experienced an internal split, as a result of which the “democratic opposition” won. In this case, Kilon opposed democracy. Pythagoras himself, according to some versions, at the time of the congress was already absent (which may indicate the correctness of the last version of the split), he moved to the Italian city of Metapont, where he died around 490 BC.
But this was only the beginning of the problems, because at first the Pythagoreans continued to hold good positions in most cities, and could hope for revenge even after the loss of their charismatic leader. And yet the internal crisis, splits between supporters of paternal customs and supporters of popular participation in politics — weakened the school. For reasons unknown to us, about 450 BC in Italy began mass pogroms with the subsequent expulsion of the Pythagoreans. This led to an exodus of the Pythagoreans to mainland Greece, after which their school disappeared for a while, dissolving into Platonism. Thus we can see that not only Thales and Anaximander, but also the Pythagorean school — took an active public position. Even in such early times philosophy was not a pure and abstract science of knowledge of the originals.
Acusmatics and mathematics
The purely philosophical school of the Pythagoreans was in close connection with the political school. There is no reason to believe that they were organizationally separated. We know that the philosophical school was divided into a lower and a higher level of initiation, known as akusmatics (“listeners”) and mathematicians (“disciples”). They, too, may have been closer to each other than it seems at first glance, especially if the mathematicians necessarily passed the akusmatikos stage. After Pythagoras’ death, two currents formed among his followers — the Pythagoreans proper (based on the mathematicians) and the Pythagorists (akusmatics). What Pythagorists-Akusmatics did later became the most famous part of Pythagoreanism, the so-called “Pythagorean way of life”. They built their lives with the help of “akusm” (verbal precepts), and all their teaching consisted in the repetition of Pythagoras’ sayings, which they treated as divine commandments. It was a school of worldly wisdom that was guided by aphorisms of the level of the Seven Sages, and if you think about it, even an order of magnitude worse. For example:
“You shall not rake the fire with your knife; you shall not step over the scales; when you leave, you shall not look back; you shall put your shoes on your right foot first, and mine on your left foot first.”
Since it was a mass part of the school, such “Pythagoreans” were much more common, and their extravagant behavior attracted more attention and became a kind of “meme”. Most of the legends about the Pythagoreans are connected explicitly with them. And if the akusmatics dealt with the religious and ritual aspects of the teachings, the mathematicians dealt with the studies of the four Pythagorean “math”: arithmetic, geometry, harmonic and astronomy. When we speak about Pythagorean philosophy, we always mean these last ones: i.e. the few elite of the Pythagorean club.
The akusmatics did not strive to create something new and develop the doctrine, but considered as wise those who have learned and can apply in everyday life the greatest number of sayings attributed to Pythagoras. Besides, akusmatics did not consider mathematicians as “real Pythagoreans”, but said that they originated from Hippas, who changed the original Pythagorean tradition, revealed the secrets to the uninitiated, and began teaching for a fee (i.e. instead of sectarianism Pythagorean mathematicians were engaged in what would later be called sophistry). Most likely, the principles of the Acusmatists were also accepted to varying degrees among mathematicians, especially if these are two stages of development within a school. The only question is to what extent the Pythagoreans were dogmatic and religious in each case.
This is the history of the emergence of the Pythagorean Union, their internal subordination and the political history of their rise and fall. But if the Pythagoreans were remembered by the ancient Greeks more by memes about eating beans, they entered the history of philosophy thanks to their mathematical teachings, to which we now turn.
Mathematical philosophy
If to believe the late Pythagorean Yamvlichus, Pythagoras once noticed, passing by the forge, that the coinciding blows of hammers of different weights produce different harmonic consonances. But the weight of the hammers can be measured, and thus a qualitative phenomenon (tonality of sound) is precisely determined through quantity. Hence he concluded that in general “number owns things”. Thus was born the view that the phenomena of nature can be translated into quantitative terms (or that quantitative changes pass into qualitative differences), and that these phenomena can be studied with the help of a mathematical language. This language itself was still very primitive at the time of Pythagoras, and many generations would pass before its application would begin to bear meaningful fruit. But it was thanks to Pythagoras that mathematics not only gained a new meaning for cognition of the hidden nature of things, but also received a new meaning as a discipline that exists separately from things. Thanks to this, Pythagoreans and mathematical scientists began to develop mathematics no longer as an empirical, but as an abstract science.
After the story of the hammers at the forge, Pythagoras realized the importance of number in music. Due to the close connection with music, an aristocratic aestheticism was embedded in the very foundation of Pythagorean teaching. With the help of the philosophy of numbers Pythagoras undertook to explain not only the visible world, but even abstract concepts of beauty and love. Such mathematical expressions as “harmonic mean” and “harmonic progression” still remind us of the connection he established between music and arithmetic. The Pythagoreans even believed that music could purify people’s souls. The Pythagorean doctrine of the harmony of the spheres is also peculiar: the transparent spheres to which the planets are attached (cf. Anaximander’s cosmology) are separated from each other by gaps that relate to each other as musical intervals; the individual celestial bodies sound in their motion (due to friction against the etheric wall), and if we do not distinguish their consonance, it is only because it is heard incessantly. Hence we can conclude that in his theory of cognition, Pythagoras insisted on the importance of differences/contrasts for the possibility of perception. Such aestheticism applies not only to music, but to any matter at all. In Pythagoreanism, harmony and beauty affect absolutely everything. Through these concepts, justice, equality and many other purely political concepts are also defined. An important fact is that Pythagoras was the first thinker who called himself a philosopher, that is, a “lover of wisdom” (but not a sage, because wisdom belongs to God alone). He was also the first to call the universe a cosmos, that is, a “beautiful order.” And although music and aesthetics play a significant role in terms of the form of Pythagoras’ teachings, but the core of his philosophy was pure mathematics, and the main contribution to philosophy he made in this field.
An introduction to the philosophical teachings of Pythagoras was well done for us by Aristotle in his Metaphysics, so we will cite his testimony in its entirety (important passages are highlighted):
The so-called Pythagoreans, having engaged in mathematical sciences, first moved them forward and, having been educated on them, began to consider their beginnings as the beginnings of all things. In the field of these sciences numbers occupy from nature the first place, and they saw in numbers, it seemed to them, many similarities with what exists and happens, — more than in fire, earth and water. For example, such a property of numbers is justice, and such a property of the soul and mind, another — luck, and, we can say, in each of the other cases exactly the same. Besides, they saw in numbers the properties and relations inherent in harmonic combinations. Since, therefore, everything else was explicitly likened to numbers in its whole being, and numbers occupied the first place in all nature, they assumed the elements of numbers to be the elements of all things, andrecognized the whole universe as harmony and number.
And all that they could show in numbers and harmonious combinations agreeing with the states and parts of the world and with the whole world order, they brought it together and adapted one to another; and if they lacked something or other, they endeavored to add it so that the whole structure was in perfect connection. Thus, for example, in view of the fact that the ten (decade), as it seems to them, is something perfect and contains in itself the whole nature of numbers, they count ten bodies carried in the sky, and since the visible bodies are only nine, so in the tenth place they place the opposite earth …. In any case, and at them, apparently, number is taken as the beginning and as matter for things, and as an expression for their states and properties, and the elements of number they consider even and odd, of which the first is indefinite, and the second definite; the one consists of both, it is both even and odd; the number itself is formed from the one, and the various numbers, as has been said, is the entire universe. Others of these same thinkers accept ten beginnings, going each time in the same row — limit and limitless, odd and even, one and many, right and left, male and female, resting and moving, straight and crooked, light and darkness, good and bad, quadrilateral and versatile. The Pythagoreans specified both how many opposites there are and what they are. In both cases, therefore, we learn that opposites are the beginnings of things; but how many of them — we learn from some Pythagoreans, and also — what they are. And as it is possible to reduce the beginnings accepted by Pythagoreans to the above-mentioned causes, it is not clearly dissected at them, but, apparently, they place their elements in the category of matter; for, according to them, from these elements, as from the parts inside, the essence is composed and formed.
The Pythagoreans maintain that things exist by imitation of numbers; seeing in sensuous bodies many properties which are in number, they caused things to be numbers,-only these were not numbers endowed with independent existence, but, according to them, things are composed of numbers. And why was this so? Because the properties which are inherent in numbers are given in musical harmony, in the structure of the sky, and in many other things. Meanwhile, for those who accept mathematical number alone, there is no possibility, in connection with their premises, of asserting anything of the kind… And it is clear that mathematical objects do not possess a separate existence: if they did, their properties would not be found in concrete bodies. If we take the Pythagoreans, there is no fault on them in this matter; however, since they make physical bodies out of numbers, out of things that have no gravity and lightness, such things that have gravity and lightness, one gets the impression that they are talking about another heaven and other bodies than sensuous ones.
In the above fragment, however, Aristotle has exaggerated. Yes, in the end everything does indeed come down to number, but physical processes are also explained by physical elements; and this is done in exactly the same way as with the philosophers from Miletus. If we turn away a little from the numerical dimension of Pythagoreanism, what we get next is a quite typical naturalistic system with material elements and tiny particles scattered in the void. In one of the extant retellings, Pythagoras says that there are five bodily figures, which are also called mathematical figures: from the cube arose the earth, from the pyramid — fire, from the octahedron — air, from the icosahedron — water, from the dodecahedron — the sphere of the universe (i.e. ether). Though it is clear that even Miletians operated with all elements, at least it is known that Anaximander and Anaximenes did it, but nevertheless innovations of Pythagoras here are obvious. He not only introduces the element of ether (it may be a special element for the very “sphere” on which the stars are attached), but actually concretizes apeiron. After all, mathematical numbers, from which all elements are distinguished, and now also all immaterial properties like nobility and love, are the literal analog of the “limitless” apeiron, which can now be handled with the help of the language of mathematics. Of course, mathematics has a supersensual character, and it is far from what Anaximander tried to do, but the logic here is roughly the same. It is likely that the theory of opposites was also internalized by Pythagoras through Anaximander. The idea of opposites plays a significant role in both of them, and against the background of the further development of this theory (see Heraclitus), they find much in common.
It also reminds us of the old natural philosophy that according to Pythagoras everything that happens in the world repeats itself again after certain intervals of time, and that nothing new happens at all. This idea (if we are to believe in the authenticity of the passages of the poet Orpheus) — Pythagoras directly borrowed it from Orphic mythology, although he could also have found it in Anaximander. The cyclical nature of the world may hint at some ideas about determinism, but we can only learn about this from Pythagoras’ followers, not from him himself.
But if Pythagoras simply developed the teachings of the Miletians, then why do many generations of researchers insist that he created a fundamentally new branch of philosophy? Of course, there are grounds for such an opinion. His rethinking of the role of aesthetics and mathematics alone would be enough to designate him as a separate school. But still the main feature of Pythagoras among philosophers was his mysticism, which perfectly overlaps with the classical “sectarianism” with special degrees of initiation of neophytes. Most importantly, he for the first time radically opposed soul and body, calling the latter a prison for the immortal soul. It was already pure idealism, and so mystical in nature that even allowed belief in rebirth (in particular, this is one of the reasons why the Pythagoreans practiced vegetarianism; suddenly your dead friend was incarnated in an animal?) The theory of the rebirth of the soul may also have been borrowed from the legendary Orpheus, as one of the variations of thoughts about the cyclical nature of the world. The very concept of rebirth already carries with it the idea that the soul can continue to exist after the death of the body, which means that it is independent of the body. In ancient Greece, it was this, the mystical side of Pythagoras’s teachings that caused the most discussion, and so he was associated with it in the first place. As Bertrand Russell quite rightly said about this idealism:
“With Pythagoras begins the whole conception of an eternal world accessible to the intellect and inaccessible to the senses. Had it not been for him, Christians would not have taught of Christ as the Word; had it not been for him, theologians would not have sought logical proofs of the existence of God and of immortality.”

But even in spite of all the innovations and this special, mystical character of his teaching, Pythagoras and his disciples did not merely attempt to give a convenient interpretation of old ideas, but also provided answers to problems unsolved by their predecessors. They clearly see these problems, and correctly establish the main ones. Their focus is still the same problem of whole and parts, of god and nature (or theology and naturophilosophy), and of those opposites which contradict each other, and which, according to Pythagoras, must at the same time end in the establishment of harmony.
«Researchers try only to indicate what the soul is like, about the body, which must receive the soul, they do not give any more explanations, as if it were possible for any soul to put on any body, as they say in the Pythagorean myths. It is the representatives of this view that say that the soul is a kind of harmony, and harmony is a mixture and combination of opposites and that the body is also made up of opposites.»
(Aristotle — “On the Soul”).
Of all the opposites, which Pythagoras puts at the basis of everything, the first pair are the limit and the limitless (apeiron). But the “limitless” cannot be a single beginning of things; otherwise nothing definite, no “limit” would be conceivable. On the other hand, the “limit” also presupposes something that is defined by it. Even here it becomes clear why it is number that is the basis of everything. For in speaking of the limit and the limit, we are already de facto engaged in counting scales. We meet these two basic principles in the Pythagorean cosmology. Here the world appears as a limited sphere, carried in the limitlessness (by the way, the Earth itself is spherical in Pythagoras). “The primordial unity, having arisen unknowingly from what,” says Aristotle, “ draws into itself the nearest parts of the limitlessness, limiting them by the force of the limit. Breathing into itself the parts of the limitless, the unity forms in itself a certain empty space or certain gaps, fragmenting the original unity into separate parts — extended units”. In order for the limitless to form a limit, it is necessary for chaotic matter to be organized into a harmonious order. Each of the worlds where instead of chaos we observe an intelligent organization of things has finally been explained. But the organization of order leads to the fact that individual objects are clearly separated from other objects, and this is only possible because of empty space. Breathing in the infinite void, the central unity gives birth to a series of celestial spheres, and sets them in motion. The doctrine that the world breathes air (or emptiness) into itself, as well as something of the doctrine of the celestial luminaries, the Pythagoreans learned from Anaximenes. The concept of emptiness was necessary to justify the motion of the elements “within something,” it also better explains the workings of contraction and expansion introduced by Anaximenes, and is necessary even at the level of geometry, as a space for the arrangement of points and lines. We have seen various hints of recognizing the void before, but never before has this issue become conceptually important. At last the void has received its full expression. Thanks to it, the picture of interaction of the elements acquires a character extremely close to the atomistic theory (each element consists not just of figures, but of tiny particles, whose figures set the “tone” of each element).
The natural philosophy of the disciples of Pythagoras
Pythagoreanism was certainly the most grandiose attempt to create a “theory of everything” that existed at the time. It is not surprising that we will find traces of Pythagorean influence throughout the history of philosophy. The Pythagorean school itself, in the broad sense of the word, lasted as long as the whole of ancient philosophy. It therefore embraces dozens of names in no way connected with Pythagoras. Here we will speak of “classical” Pythagoreanism, still bound by a direct chain of succession leading back to Pythagoras himself. And the major figures on our list are:
- Hippas — Pythagorean apostate, leader of the “democratic opposition” and scientific line of Pythagoreanism. A philosopher who synthesized the views of Pythagoras and the Miletian school.
- Alcmaeon — Physician-surgeon who empirically established that the brain is the center of concentration of the mind.
- Philolaus — Pythagorean, systematizing the teachings of Pythagoras, Hippas and Alcmaeon, who later passed on the knowledge to Plato.
Some of what we have said above about the philosophy of Pythagoras — we learn only from the writings of his disciples. We have selected only what seems most similar to the fundamental theses of the school, without which it is impossible to imagine either the teachings of Pythagoras himself or the opinions of his disciples. We shall now set forth the specific characteristics of each of the disciples separately, and summarize the results for the Pythagorean school taken as a whole.

The Pythagorean Judas
As already mentioned, at some point Pythagoras had a “democratic” opposition within the sect. Some guy named Hippas of Metapontus (c. 530-480) violated the prohibition against non-disclosure of secrets, for which he was expelled from the elite club. Subsequently, the Pythagorean tradition used this name as a synonym for essential evil and treason. We have already mentioned this when we talked about the attitude of the Acusmatists to mathematicians as sophists who sold the wisdom of Pythagoras for money. In that case, not only “enlightenment”, but even sophistry, and the typical attitude towards it — arise within the Pythagorean union. Of course, this sounds strange, given the fact that the Pythagorean school was the largest school in Greek history, a massive school with extensive regional representation. This already automatically implies a great deal of openness. But most likely, the school admitted only people of noble origin (though not only specialized scholars), which was already a significant step forward; and Hippas brought this enlightenment trend to the next stage of development. Hippas was notorious in later centuries, but even the ancient Greeks suspected that most of Pythagoras’ achievements were actually Hippas’ discoveries, so powerful was he supposedly as a philosopher. Sometimes Hippas was even called the founder of the “mathematical” (i.e., purely scientific) branch of the school. But if this is true, then Pythagoras himself really belonged rather to the “akusmatists”, and all the best achievements of the school are the fruit of the activities of apostates.
In addition to participating in the schism and “divulging secrets” Hippas became hated also because, besides proportions and commensurability of things, he revealed to the public the doctrine of incommensurability (or even irrational numbers). The Pythagoreans carefully concealed this phenomenon in mathematics, for they saw the source of the world’s orderliness and reasonableness in numbers. Numbers consist of identical units, and the world is based on a unit. And suddenly it turns out that at least two different units, irreducible to each other, are at the basis of the world. So the irrational, the irrational now finds itself at the heart of the world. The Pythagoreans did not know what to do about this; the phenomenon of incommensurability was destroying their worldview. Therefore, after the exile, Hippas was even cursed, and according to the legend of the Pythagoreans themselves, he sank in a shipwreck, allegedly as a punishment from the gods.
Hippas is known as a democrat not only because he spread knowledge to all comers. He is also listed among the leaders in the political division of the Pythagorean community. As the later Pythagorean, Yamvlichus, writes about it:
When they initiated the schism, the other inhabitants of Croton immediately began to join the distribution. From among the most oligarchic “thousand” Hippas, Diodorus and Theagus were in favor of all citizens of Crotona to participate in public office and the national assembly, and that the archons reported in their activities to the people’s representatives, elected by lot from among all citizens. They were opposed by the Pythagoreans Alkimachus, Dinarchus, Meton and Democedes, who opposed the overthrow of the fatherly system. Those who spoke in defense of the masses won.
And so, the subsequent persecutions can be connected with the reaction of the local aristocracy against the attempts to introduce a democratic system. Perhaps the traditional Pythagoreans were able to resist at the expense of the alliance with the aristocracy, and the democrats became victims of the first wave of pogroms, as a result of which they were “expelled” from the ranks of the school, and as a result of which Hippas himself died. Otherwise, it’s hard to understand how the winner in an internal schism was suddenly victimized. Then it would appear that the conservative branch survived the first wave of pogroms, and was expelled from Italy after the second wave. It is extremely difficult to reconstruct the actual version, due to the lack of additional sources.
In his philosophy Hippas is also sharply oppositional. As if returning to the bosom of the Miletian school, he taught that the beginning of all things was elemental, and that element was fire. At the same time, he agreed that number was also at the heart of nature, conducting quantitative experiments with sound in much the same way as Pythagoras did (only instead of hammers — iron disks). Apparently, for Hippas, number is not the beginning itself, but only a manifestation of the divine nature. Mathematics is the language God used to create the visible world. Or, as Hippas himself put it, “the distinguishing tool of the creator god.” His God, then, has reason and discernment; he is a creator in the most literal sense of the word “creation.” The creator god himself, as well as the soul of all beings, and even as the material universe, are all inherently fire. In opposition to Pythagoras, Hippas teaches that the universe is one and spatially finite (which does not invalidate its emptiness or its perpetual motion). The fire of which it is composed is transformed by densification and rarefaction. This synthesis looks as if it were an answer to the teaching of Pythagoras, its inner opposition, and an attempt to pass from the speculative beginnings to the unconditional material primary basis.
Pythagorean medical school
One of Pythagoras’ most famous disciples became the founder of the first medical school in Greater Greece (the Crotonian School). He is known as Alcmaeon (ca. 515-460 BC), and is listed as one of the first serious scientists in the modern sense. But it should be noted here that there was a major medical man named Calliphon who lived in Crotona even earlier, and who after the appearance of Pythagoras became a supporter of his teachings. Apparently he was the chief priest of Croton and a man of great importance in civil affairs. He also had a son who became a major medical man, whom Herodotus later called “the most skillful physician of his time,” his name was Democedes, probably a contemporary of Alcmaeon. In his youth he came to the island of Aegina, where, thanks to his talent and diligence, he soon gained fame as a skillful physician. Leaving Aegina, he went to Athens, and then worked at the court of the Samosian tyrant Polycrates. After his overthrow was sent to Sardes, then to his court he was summoned by Darius I. Having cured the king of a disease of the legs, and the queen Atossa — from a chest disease, Demoked got into great favor with the Persian king, who generously rewarded him for curing his ailments. From there he returned to his homeland, despite Darius’ entreaties to remain with him as his life-medic. Returning to his native Croton joined the party of aristocrats. There he joined the society of Pythagoreans, married the daughter of the famous Greek athlete Milon of Croton. However, during a revolt against the Pythagorean oligarchy, Demokedes died. Demokedes, along with Alcmaeon, was at the head of the oldest flourishing medical school in Greece. But we do not know the details of the teachings of Demokedes and his father, but we do know the details of Alcmaeon’s teachings.
Alcmaeon’s theory of medicine was based on Pythagorean harmony and the theory of opposites. In the theory of opposites itself, Alcmaeon also made an important step forward. Whereas previously the set of opposites had always been limited and concretized (equally in both Anaximander and Pythagoras), he now speaks of an infinite number of very different opposites. Any idea about the simplest subject can give rise to its own antithesis. And by saying the phrase “most human things are binary ‘ — he not only took a step towards the future teaching of Heraclitus, but also opened the road towards sophistry (see ’Binary Speeches”). In the lists of philosophers who proposed different quantities of “beginnings” of things, it is said of Alcmaeon that he assumed two beginnings. What they are, we do not know, but we can assume that they could be “positive and negative”, well, or, following his theory of equilibrium, these beginnings could even be “democracy and monarchy”. The latter is of particular interest, because it allows us to conclude that, like Hippas, Alcmaeon belonged to the “democratic opposition” within the Pythagorean Union (and then he was hardly an associate of Democedes). According to his theory, human health is preserved through balance, for the domination of one opposite acts perniciously on the other, and therefore disease arises. If we believe the book “Opinions of Philosophers” (Pseudo-Plutarch), Alcmaeon called this equilibrium of the elements of the organism “democratic equality”, and called “monarchy” among them the cause of disease. It is curious to compare the theory of balance with ancient Chinese ideas about medicine, which also appealed to the balance of “yin-yang”, and made the same conclusions about the origin of diseases.
Probably in Greek philosophy he was the first to say that man differs from other animals by the fact that only he thinks, while other animals feel but do not think (even now, when we know that this is wrong, the same division is given, for we still distinguish between “thinking in general” inherent in animals and thinking specifically human). According to his views — the primordial part of the soul is in the brain. He came to this conclusion through research (the same “empiricism” as Thales’ conclusions about magnetism) on the nervous system and tracing the sensitivity of impulses from the endings and closer to the center. This is the more interesting because the influence of Egyptian medicine on Greek medicine is obvious to us; Egypt was inordinately more advanced in every respect. However, the Egyptians considered the heart to be the center of emotion, personality and intellect. For this reason, in mummification, the hearts of the dead were preserved, while the brain was scraped out and discarded as a useless organ. This example illustrates the advantages of the emerging Greek empiricism.
One might think that Alcmaeon, even more learned than any of his predecessors, a supporter of progressive views in politics and the enlightenment of the masses, should himself be less superstitious than the Pythagoreans. Except that in reality we see a metaphysician like Thales, Pythagoras, or Hippas. He holds that truth is available only to the gods, and that men are left to “the things of men,” which, as we saw above, can only be judged in two ways. He also separates the divine and human world (i.e., the whole and the parts), and logically he joins the Pythagorean dualism of body and soul. Alcmaeon’s understanding of the soul itself is typical for his time. Like his predecessors, he calls the soul self-moving by nature and possessing eternal motion; for this reason, it is immortal and godlike. Alkmeon directly compared the properties of the soul with the properties of the “supralunar” world, because the stars also have eternal motion. And from the divine nature of the luminaries he made a typical conclusion that the gods and the luminaries are one and the same.
But still, as a physician, Alcmaeon was obliged to deal not only with philosophy, but also with natural philosophy. Not only the world above the moon, but also the world of the earth. From such reasoning, except for what has already been said about the location of the mind in our brain, he writes in a naturalistic sense about the five sense organs (we quote Theophrastus’ work “On Sensations”):
Hear, he says, with the ears, because there is a void in them: it sounds (and the sound is produced by the cavity) and the air echoes. They smell with the nose, drawing pneuma to the brain at the moment of inhalation. Tastes are distinguished by the tongue: being warm and soft, it melts food by its warmth [= mellows out its “flavor juices”], and through its porosity and tenderness absorbs them, and transmits them through the pores to the brain. The eyes see through the surrounding moisture. That the eye contains fire is evident, for when the eye is struck, fire flashes [“sparks fly”]. They see by means of the shiny and transparent body in the eye, whenever it glows, and the clearer it is, the better. All the senses are in some way attached to the brain, and are therefore injured by its concussions and displacements, as it plugs the channels through which the sensations are transmitted. About touch, however, he said nothing.
There are other descriptions of Alcmaeon’s opinions similar to this, which also include theories about the conception of a child, typologizations of animals according to the way in which offspring are born and fed, speculations about how gray hair arises, etc. But they are all described in a similar naturalistic sense. If we combine the positions of Hippas and Alcmaeon, and contrast them with Pythagoras himself, the result of consistent criticism is a de-mystified version of Heraclitus’ philosophy. This fact is extremely important for understanding the whole genesis of the history of philosophy.

Heirs of Pythagoras
Of the minor Pythagoreans we can mention, for example, a woman named Theano, who wrote the works: “On Pythagoras”, “On Virtue to Hippodamus of Fury”, “Women’s Exhortations”, “Utterances of the Pythagoreans” and “On Piety”. Moreover, in this last one, strangely enough, she acts as an interpreter of Pythagoreanism in the physical sense! Namely, she says:
«Many Hellenes, as I know, think, as if Pythagoras had said that everything is born of number. But this doctrine is perplexing: how is that which does not even exist thought to be generating? Meanwhile he said that everything does not arise from number, but according to number.»
It turns out that even for Theano numbers do not really exist! But she saw Pythagoras personally, and in some versions is even considered his wife and mother of the next head of the Pythagorean school — Telawg. By the way, the latter was even considered to be Empedocles’ teacher before he left the school. Various surviving letters of Theano are devoted to domestic concerns: how a woman should bring up her children, how she should treat her servants, and how she should behave virtuously towards her husband (rather primitive recommendations about the necessity of obedience). Theano’s father named Brontine, who according to some versions was her husband (rather than her father) instead of Pythagoras, is believed to be the author of some Orphic poems, among them “On Nature” and “The Veil and the Net”. Various Orphic poems have also been attributed to many other Pythagoreans, which either confirms their direct dependence on the Orphics or means that Orphism was indeed fabricated by the Pythagoreans. But more likely, of course, is the former.
It is also worth remembering the philosopher Hippon (c. 490-430 B.C.), who bore the nickname “godless”. According to one account, Hippon considered water to be the beginning of everything, according to others — water and fire, according to others — earth (note that in all versions these are not numbers); but the most authoritative version is considered to be the version with fire and water beginnings; at the same time they were considered to be synonymous with hot and cold, the struggle of which created everything in the world, which brought Hippon’s teaching closer to such philosophers as Anaximander, Anaximenes (and even Hippas, Xenophanes and Heraclitus). In this section, he complements “elemental” philosophy by standing between Thales and Heraclitus. Hippon devoted considerable attention to questions of biology and medicine, in particular to the problems of embryology, the origin of boys and girls from different kinds of sperm (in which he directly continued the themes touched upon by Alcmaeon); he tried to explain the origin of twins. He wrote also on matters of botany. Like Alcmaeon, he emphasized the significance of the number “seven” for the stages of human life (e.g. twice seven is the age of human adulthood). He identified the soul either with the brain or with water, since semen, which is accessible to our observation, is also composed of moisture, and meanwhile from it, he claimed, the soul is born. Hippon proved to be a very authoritative writer on embryology, and his opinions would long enter the canon of philosophy. In the example of Hippon we can see both the influence of Alcmaeon and that of Hippas. But still he appeared more interested in biology as a science, and did not develop the tendencies laid down into a doctrine analogous to the later philosophy of Heraclitus. He apparently tended to synthesize Pythagoreanism and the teachings of the Miletians, developing Hippas in this particular, “spontaneous” direction. Among the major Pythagorean biologists, whose opinions we will not describe in detail, there was also Menestor, and a rather original version of the argumentation in favor of emptiness (adopted by Democritus) was put forward by Xuphus.
Such a number of “apostates” from the official line of Pythagoreanism, suggests that this is nothing more than a myth, and that Pythagoreanism was originally very heterogeneous, and has much more in common with the Miletian school than it appears. Hippon thus appears to be an exceptional case, for he is the only one of the whole group of pious philosophers who is called “godless.” The reasons for this appellation are unknown, and it may well be that they have nothing to do with real atheism, but in any case this characterization is not insignificant.
A systematizer of Pythagoreanism
The most famous Pythagorean, who goes much farther back in chronology, is Philolaus (ca. 470-400 B.C.). We are already getting a little ahead of ourselves by bringing out his figure; we will refer to Philolaus later when we talk about Plato and Democritus. To realize how far ahead we are, we may note that it is from Philolaus (or from his pupil, which is more likely) that Plato buys the Pythagorean books, and begins to form his own philosophy. Almost all of what we have stated as the philosophy of Pythagoras himself was actually stated by Philolaus, and therefore we will not recount the things we have already mentioned before (such as the reasoning about the limit and the limitless, the body as the tomb of the soul, etc.). Let us assume that the main line of Pythagoreanism is borrowed by Philolaus in full, being orthodox. But of the new opinions this one stands out particularly vividly:
“In his view, everything is accomplished by necessity and according to the law of harmony.”
Philolaus turns out to be the first Pythagorean to express strict determinism (this does not mean that others did not hold the same opinion). It is true that in different forms we have seen this thesis in literally all philosophers from Miletus. Despite being considered the main source on authentic “numerical” Pythagoreanism, and being, shall we say, a Pythagorean dogmatist, Philolaus (just like Hippas and Hippon), places fire in the middle of the universe, which no longer looks like a mere coincidence. This fire was placed around the center, which he calls Hestia (the hearth) of the universe, the house of Zeus, the mother and altar of the gods, the bond and measure of nature. But he also recognizes another fire — lying above everything and encompassing the universe. Something similar was already found in the fire philosophy of Hippas, where fire appeared in different hypostases, but here, however, Anaximander’s “fire” is clearly visible. The same fire that was outside the “celestial sphere” and seeped through the openings of the firmament as the visible stars. But Philolaus’ concept is important and even original, as the first image of a cosmology where the Sun would be at the center of the world, instead of the Earth. The abundant use of metaphors with the names of the gods, which has not yet been seen in the rest of the Pythagoreans, is striking.
It is thanks to Philolaus that we still speak today of the figures of numbers (square, cube), and it was Philolaus who first clearly distinguished not only between body and soul, but also between God and nature, in terms of the hierarchy of power and subordination between them. If later sources are to be believed, he could even distinguish between form and matter, naturally considering matter as the subordinate element and form as the higher, incorporeal, eternal and divine. Of course, all this may be a Platonic hoax rather than an original source; but we will not deny such a possibility altogether. The subject matter of Philolaus’ treatise is extensive: from ontology he passes to gnoseology, cosmology and astronomy, touches upon other exact sciences, and ends with physiology and medicine. The latter he deals with in a very generalized sense, but nevertheless, it can be considered the completion of the systematization of the entire Pythagorean heritage, including even the teachings of the oppositionalists.
Summarizing
Alcmaeon, Theano, Hippon, and Philolaus are perfectly consistent with each other, and yet none of them, as we can see, look like what the Pythagoreans must have looked like according to common patterns. They all engage in classical natural philosophy, continuing the themes begun in Ionia, but attempting to use mathematics to understand the essence of the world. Yes, this led them essentially to a conscious idealistic interpretation of the dualism of soul and body, but we can easily find all the prerequisites for this among the Miletians as well. Of course, it is their idealistic side that they are remembered as a “meme”. Besides, Philolaus, systematizing the teachings of Pythagoras, laid special emphasis on idealism, and our subsequent ideas about the school are based primarily on Philolaus’ writings.
Generally speaking, of the so-called “Dosocratics” it was Pythagoras and the Pythagoreans who were so influential that we will find their followers right up to the end of antiquity, even in the Roman Empire. But even in the early epoch the Pythagoreans were so numerous that it was impossible to do philosophy in Italy without crossing paths with them. Not only in Italy, but even in mainland Greece, their fame was immense and their influence truly omnipresent; and such traditionally hostile figures as Plato and Democritus could equally be considered half-Pythagorean. Still later, as we may have noticed, Aristotle had to argue with them. And in the course of further exposition we will constantly notice the influence of Pythagoras on almost every philosopher. Even Herodotus called Pythagoras “the greatest Hellenic sage”, and Hippocrates used Pythagorean medicines. About exclusive popularity of Pythagoras and his doctrine in ancient Hellas testify and data of numismatics. In 430-420 BC in the city of Abdera (the birthplace of Democritus and Protagoras) minted coins with the image of the philosopher and the legend “ΠΥΘΑΓΟΡΗΕ”. The case is unprecedented for this period, as it represents the first portrait on a coin, at least the first signed portrait.
If we try to outline the place of Pythagoreanism on the level of the scheme, we see how this school, trying to solve the problem of the bifurcation of the world, in fact, only aggravated this bifurcation. The pantheism of the Miletians may not have been true pantheism, but they still tried to pretend that the world was essentially one. The Pythagoreans do not even doubt that the world is dual, but they hope to patch up this problem with the doctrine of “harmony”. By introducing a colossal number of innovations, they opened the way for the creation of numerous new schools of philosophy, and armed them with the tools to discover more contradictions in the pantheistic view of the world as a whole. It was from this angle that they were perceived by all contemporaries who attempted to recover the Philosophy of the Whole. But taking into account the influence of Pythagoras himself, all these attempts were built on a pronounced idealistic basis, in contrast to the still uncertain positions of the original Miletian school. In the scheme of Hegelian triads, this looks like thesis (the uncertain idealism and pantheism of Miletus) — antithesis (the certain idealism and dualism of Pythagoras) — synthesis (the certain idealism and pantheism of Pythagoras’ critics).
Next part.






